Models of Projective Geometry
For me the most enticing facet of projective geometry is the profound way in which it treats duality. Duality is the notion that certain fundamental distinctions have similar structure in their complementary forms. In comparing a form with its dual, the basic structure remains even though the roles of the forms reverse. Inside and outside. Convex and concave. Yin and yang. In 2D (two-dimensional) projective geometry, point is dual with line; in 3D point is dual with plane while lines are self-dual. The relationship of duality is so penetrating and pervasive in projective geometry, that we might consider it the geometry of fundamental duality. It provides a geometrical stage upon which duality can be studied in a pure form.
Another profound aspect of projective geometry is its elementary treatment of incidence where one considers the join (∨) and meet or intersection (∧) of two basic geometrical objects such as point, line, plane, and hyperplane. The most fundamental correspondence of geometrical forms associates points and lines in dual arrangement: the points on a line form a range and the lines through a point form a pencil. The correspondence between a pencil and a range is a basic projection. Next a perspective relation joins a pencil with two ranges or a range with two pencils; that is, by combining two elementary projections. Such a perspectivity maps points to points, or dually, lines to lines as shown in the figure. 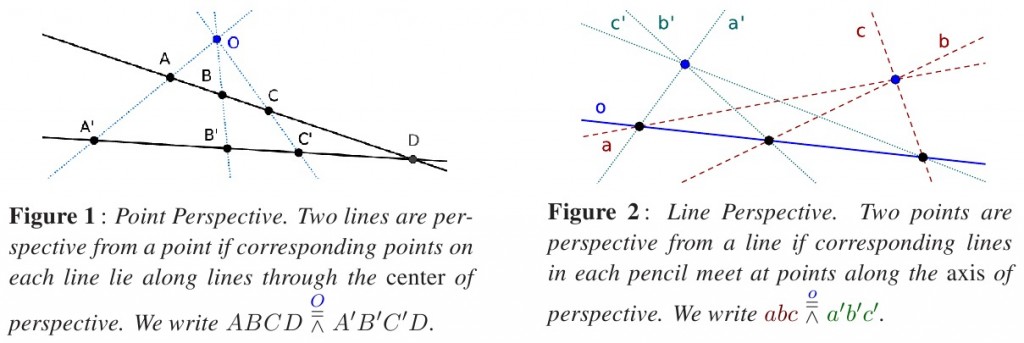
In the essay “Design Strategy” in Buckminster Fuller’s book Utopia or Oblivion, he includes projective geometry in his list of recommendations for a curriculum of design science. The connection between projective geometry and design thinking is an area that deserves more attention.
A Catalog of Models of Projective Geometry
The rest of this essay tersely describes a broad listing of some of the more basic models of projective geometry. Models are a powerful tool for learning and for understanding as explained in my essay about the Importance of Model Thinking (based on Scott E. Page’s course). The models included below should provide an introduction to and an overview of projective geometry for those new to the subject (Note: some of these models require background knowledge that is not explained here. They are indicated with a ![]() . I encourage you to skim or skip such models, but to read on as later models may be more tractable.) I hope the experts will find the succinct summary and references useful. Although this list is fairly comprehensive, there are many models that are necessarily omitted. If you have a favorite model, please post a comment about it.
. I encourage you to skim or skip such models, but to read on as later models may be more tractable.) I hope the experts will find the succinct summary and references useful. Although this list is fairly comprehensive, there are many models that are necessarily omitted. If you have a favorite model, please post a comment about it.
- Configurations. A configuration (pn,lm) is a set of p points and l lines such that each of the points lies on n lines and each of the lines contain m points. So there are n lines through each of its p points and m points lie on each of its l lines. For example, (43,62) is a complete quadrangle and its dual (62,43) is a complete quadrilateral. If p = l and m = n, the configuration is self-dual. E.g., a triangle is (32). A finite projective plane of order n PG(2,n) is a self-dual configuration of the form (n2+n+1)n+1 if such a configuration exists (which happens when n=pk where p is prime and k is a positive integer). Most descriptions exclude the case where n=1 which would give a triangle (32). When n=2, we get the fano plane (73). This treatment emphasizes that there are many finite projective planes. Configurations are easy and fun especially since finite projective planes require non-straight lines to draw on paper. For more on configurations see [Coxeter2003, p. 233] and [Polster, pp. 27-38]; for more on finite projective planes see [Polster, pp. 5-7, 67-124 (includes many beautiful drawings)], [Coxeter1989, pp. 233-4] and [Coxeter2003, pp. 91-101].
 Block Designs. A nice characterization of finite projective planes is provided by the subject of block designs (which originated as part of experimental design). Namely, the projective plane of order n PG(2,n) exists if and only if an (n2+n+1, n+1, 1)-design exists if and only if there is a complete orthogonal family of Latin squares of order n (I studied Latin squares with Thomas Zaslavsky in an undergraduate combinatorics course at Binghamton). See [Roberts, pp. 356-405].
Block Designs. A nice characterization of finite projective planes is provided by the subject of block designs (which originated as part of experimental design). Namely, the projective plane of order n PG(2,n) exists if and only if an (n2+n+1, n+1, 1)-design exists if and only if there is a complete orthogonal family of Latin squares of order n (I studied Latin squares with Thomas Zaslavsky in an undergraduate combinatorics course at Binghamton). See [Roberts, pp. 356-405].
- Axioms provide another approach to characterize projective geometry. This list defines a projective plane (see [Polster, p. 5]).
- Axiom of joining. Any two distinct points are incident with a unique line.
- Axiom of meeting. Two distinct lines intersect in a unique point.
- Axiom of a quadrangular set. There are four points of which no three are collinear (meaning no three lie on the same line). This axiom effectively defines a quadrangular set.
- Following [Polster, p. 67] and [Coxeter1989, p. 256], here is an axiomization for projective space (meaning 3-dimensional or 3D):
- Axiom of joining. Any two distinct points are incident with a unique line.
- Axiom of transversals to triangles. If a line does not include any of the vertices of a triangle but it intersects two of its sides, then it intersects the third side of the triangle.
- Axiom of minimal extent of lines. Each line contains at least three points.
- Central projection. [Hefferon] describes six models of the projective plane based on central or Gnomonic projection.
- In the first three models, P can represent a projector, a painter, or a pinhole camera which projects the source scene S to an image plane I. The geometry of the image plane I is projective.
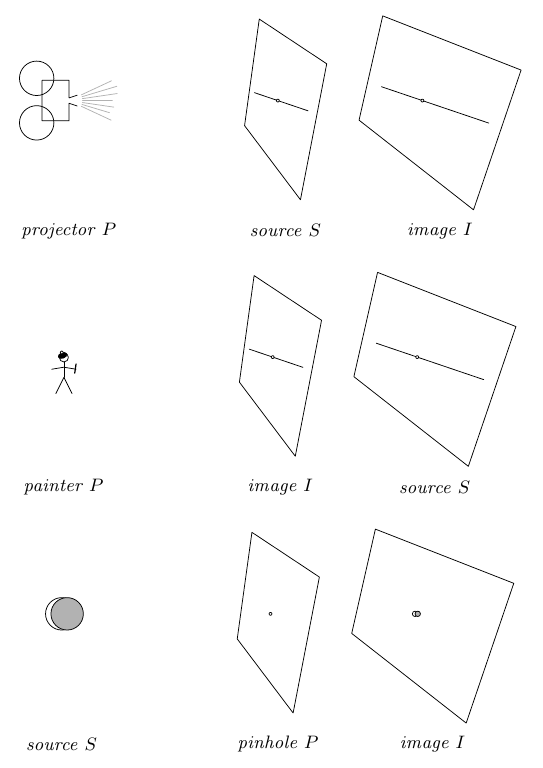
PIS Central Projections. Adapted from [Hefferon].
- Hemisphere Model. In an attempt to simplify these three models, we can place P at the center of a hemisphere and map any point X in space to the point on the hemisphere on the line joining P and X (l=P∨X). Points on the equator get mapped to two points on the hemisphere, so they must be treated specially. Also see [Polster, p. 227-8].
- Sphere Model. We can do even better with a whole sphere and mapping any point X to the two antipodal points where the sphere meets the line joining X with P (l=P∨X). The model treats the two antipodal points as one “point” and a great circle (a circle on the sphere whose center is also the center of projection) as a “line” in the projective plane. Also see [Polster, p. 225].
- Extended cartesian plane. Continuing the analysis by choosing the unit sphere (meaning radius of 1) and the tangent plane z=1 so it touches the plane at the sphere’s North pole. The model now maps points X in space to points on the plane z=1 (where l=P∨X intersects z=1). There is a problem with points which map to the equatorial points on the sphere: they are parallel to the plane z=1! So the model imagines that in each direction around the equator there is an “ideal point” (sometimes called a “point at infinity”) in the plane z=1 which corresponds to the two equatorial points. Since the totality of these “ideal points” map to the great circle known as the equator, the collection of “ideal points” forms an “ideal line” (which is sometimes called the “line at infinity”). See [Wildberger] for a nice video introduction to projective geometry that explains this model.
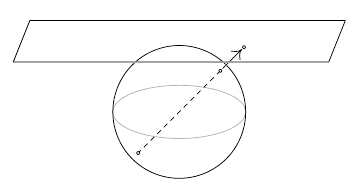
The unit sphere tangent to the z=1 plane. Adapted from [Hefferon].
The sphere model gives a concrete finite perspective on abstract “infinity”. From this perspective “infinity” is just a poetic expression of a concrete reality. It could be that all uses of the word “infinity” in mathematics are like this. See [Zeilberger] for another ultrafinitist interpretation of infinity in mathematics.
The traditional description of this model starts with the traditional Euclidean plane (or more generally the affine plane) and affixes a single “ideal point” to each set of parallel lines. Each of these “ideal” points lies on an “ideal line”.
- In the first three models, P can represent a projector, a painter, or a pinhole camera which projects the source scene S to an image plane I. The geometry of the image plane I is projective.
- Bundle models of the projective plane. In 3D space, a bundle is the collection of all the lines and planes through a given point O (which we can think of as the origin or the center of the bundle). The modern algebraic treatment of projective spaces springs from this fruitful model.
- “Points” are represented as lines through O. “Lines” are represented by planes through O. The “line” joining two “points” is the plane perpendicular to them both. The intersection of two “lines” is the line perpendicular to their two normals (the normal of a plane is the line or direction or vector perpendicular to it).
 Perpendicular Vectors. In the bundle model we can represent points and lines as vectors anchored to the origin at O. A “point” is simply represented by a vector. A line is represented by the normal vector to a plane. A point is incident with a line if their dot product is 0 (that is, they are perpendicular). The line joining two points is given by the cross product of the vectors representing the points. The intersection of two lines is the vector given by the cross product of the vectors representing the lines (each normal to its plane). I find it remarkable and lovely that the cross product serves as both meet (∧) and join (∨) in this model: it emphasizes the duality at the vector operation level!
Perpendicular Vectors. In the bundle model we can represent points and lines as vectors anchored to the origin at O. A “point” is simply represented by a vector. A line is represented by the normal vector to a plane. A point is incident with a line if their dot product is 0 (that is, they are perpendicular). The line joining two points is given by the cross product of the vectors representing the points. The intersection of two lines is the vector given by the cross product of the vectors representing the lines (each normal to its plane). I find it remarkable and lovely that the cross product serves as both meet (∧) and join (∨) in this model: it emphasizes the duality at the vector operation level! Homogeneous coordinates model. This is effectively an algebraic representation of the perpendicular vectors model. Since our bundle is in 3D space, we can represent both points and lines as ordered triples since they are both represented by vectors. These are scale independent and so are homogeneous.
Homogeneous coordinates model. This is effectively an algebraic representation of the perpendicular vectors model. Since our bundle is in 3D space, we can represent both points and lines as ordered triples since they are both represented by vectors. These are scale independent and so are homogeneous.
- Extended cartesian space. In ordinary Affine (or Euclidean) 3-space, we can add an ideal point for each set of ordinary parallel lines. In any given ordinary plane, the collection of its ideal points form an ideal line. All those ideal points and lines form an ideal projective plane, the so-called plane at infinity. See [Coxeter2003 pp. 103-109] and [Richter-Gebert pp. 209-11].
- A very abstract approach (see [Busemann and Kelly p. 1] and [Richter-Gebert p. 36]) is to remove special cases such as the distinction between intersecting or parallel lines from Euclidean (or Affine) geometry. This model sees projective geometry as a more general geometry with a minimum of special cases.
 Vector subspace model of projective spaces. Given any n+1 dimensional vector space over any arbitrary field F, the projective space of dimension n can be represented by its k dimensional subspaces, k=0,1,…,n. When k=0, the trivial vector subspace {0} determines the empty projective subspace. When k=1, the collection of 1-dimensional subspaces represent the “points” of our projective space. When k=2, the collection of 2-dimensional subspaces represent the “lines” of our projective space. When k=s, the collection of s-dimensional subspaces represent the s-planes of our projective space. If an s-plane is contained in an t-plane, we say that it lies on or is incident with it. This containment relation forms a lattice in our projective space. The lattice operations of join (∨) and meet (∧) give the incidence structure of the space. See [MacLane and Birkhoff, pp. 592-595].
Vector subspace model of projective spaces. Given any n+1 dimensional vector space over any arbitrary field F, the projective space of dimension n can be represented by its k dimensional subspaces, k=0,1,…,n. When k=0, the trivial vector subspace {0} determines the empty projective subspace. When k=1, the collection of 1-dimensional subspaces represent the “points” of our projective space. When k=2, the collection of 2-dimensional subspaces represent the “lines” of our projective space. When k=s, the collection of s-dimensional subspaces represent the s-planes of our projective space. If an s-plane is contained in an t-plane, we say that it lies on or is incident with it. This containment relation forms a lattice in our projective space. The lattice operations of join (∨) and meet (∧) give the incidence structure of the space. See [MacLane and Birkhoff, pp. 592-595].- Abstract naming. This is just a notational convention to represent projective geometries, but names are models of a sort too. The projective space of dimension n over the algebraic field F is denoted PG(n,F).
Conclusion
As you can see there are many, many models for projective geometry. Since a complete enumeration of projective spaces has never been compiled, there are many more models to be imagined and constructed. If you have any questions about these models or know of any other projective models, please post a comment. I look forward to discussing them!
Postscript
One of my many reasons for writing this essay is to provide background information for the Harmonic Perspective paper that Jeannie Moberly and I prepared for the 2012 Bridges Conference and Proceedings. I wrote a Harmonic Perspective page to collect information about our work on the subject.
References
- Herbert Busemann and Paul J. Kelly. Projective Geometry and Projective Metrics. Dover, 2006.
- H. S. M. Coxeter. Introduction to Geometry. Wiley, second edition, 1989.
- H. S. M. Coxeter. Projective Geometry. Springer, second edition, 2003.
- Jim Hefferon. Linear Algebra see “Topic: Projective Geometry” in the chapter “Determinants”. On-line textbook with a free license. Accessed 10 July 2012.
- Saunders MacLane and Garrett Birkhoff. Algebra. AMS Chelsea Publishing, third edition, 1999.
- Burkard Polster. A Geometrical Picture Book. Springer, 1998.
- Jürgen Richter-Gebert. Perspectives on Projective Geometry: A Guided Tour Through Real and Complex Geometry. Springer, 2011.
- Fred S. Roberts. Applied Combinatorics. Prentice-Hall, 1984.
- Norman Wildberger. MathHistory8: Projective geometry (YouTube video). Accessed 22 July 2012.
- Doron Zeilberger. “Real” Analysis is a Degenerate Case of Discrete Analysis. Accessed 10 July 2012.

A splendid and illuminating piece of work. Sorry I can’t attend Bridges this year. I would enjoy attending your presentation. Hatton’s book on The Principles of Projective Geometry is terrific. I am reminded that the underlying geometry of tensegrities is projective geometry, specifically 3D projective geometry. Good job.
Hi CJ, I see you are ready for your conference. In his earlier years, I can imagine that your grandpa would probably be right there with you. Maybe Ryan to some degree, and I could follow for awhile, so I am glad to say that you have stretched my mind tonight.
Have an enjoyable trip with Jeannie.
Love and God bless you for using your intelligence wisely. Mom
On the surface this looks like it could be a step backwards from the usefulness of Synergetics. There’s a level of complexity here that i’ve so far found confusing. Part of that complexity, of course, is the presence of points, lines, and planes.
Another possible perspective is, of course, that it is a transition between Euclidian geometry and Synergetics. As such, it may serve to satisfy the needs of some people for linear complexity.
One thing i liked a lot was the initial handling of duality. It’s easy to turn the idea of duality as a stumbling block into an inflexible (and thus useless) doctrine. Duality, and its resultant dialectic materialism can be involved in some very unhealthy social constructions. However, our universe always includes the phenomena associated with polarity. By systematically ignoring anything associated with dialectics, we fall into the danger of failing to understand the essential concepts of polarity.
These are some initial thoughts. It’s nearly certain that there are many other ways to understand projective geometry as presented here. And, of course, the paper itself needs to be read. Now that the heaviest part of conference season is finished, there is more time to consider this and also to work on scheduling future events if possible.